[最も共有された！ √] (1 2/n)^n limit 697704-Limit ln(2 n/n+1)

 It follows that for n ≥ 2 we have 2n ≥ (n 2) = n(n − 1) 2 Thus for n ≥ 2 we have 0 ≤ n 2n ≤ 2 n − 1 For n large, we have 2n ≥ n2 This can be easily proved by induction for n ≥ 4 I would like to say then that n 2n = n 2√n 1 2n − √n, and the first fraction is bounded above by 1, while the second approaches 0Type Notes Uploaded By tomango8 Pages 56 This preview shows page 36 39 out of 56 pagesCentral Limit Theorem (Convergence of the sample mean's distribution to the normal distribution) 2 n−1 (n − 1) 2 n − 1 So we can 2well estimate S when n is large, since Var(S) is small when n is large Remember, 2the χ distribution characterizes normal rv with known variance You need to

2

Limit ln(2 n/n+1)

Limit ln(2 n/n+1)-N n4 lim n!1 2n3 (n23n6)2 n n4 = lim n!1 2n 3 (n2 3n 6)2 n4 n = lim n!1 2n 3 n n4 (n2 3n 6)2 = 2 1 = 2 Therefore, since the limit is nite and the series P n n4 = 1 n3 converges, the Limit Comparison Test implies that the given series converges as well 16For which values of xdoes the series X1 n=0 (x 4)n 5n converge?Thread starter #1 K karseme New member 15 How could I calculate $\displaystyle \lim_{n \rightarrow \infty}{(\sqrt(n^2n) \sqrt3(n^3n^2))}$ Everything that I tried I always got infinite forms or 0 in denominator I don't

Evaluating Frac1 N 2 1 2 Frac2 N 2 2 2 Dots Frac N N 2 N 2 Using Riemann Sum Mathematics Stack Exchange

The infinite series whose terms are the natural numbers 1 2 3 4 ⋯ is a divergent series The nth partial sum of the series is the triangular number ∑ k = 1 n k = n 2, {\displaystyle \sum _{k=1}^{n}k={\frac {n}{2}},} which increases without bound as n goes to infinity Because the sequence of partial sums fails to converge to a finite limit, the series does not have a sumThis proves (2), in view of the definition (26) of "for n ≫ 1" ¤ The argument can be written on one line (it's ungrammatical, but easier to write, print, and read this way) Solution Given ǫ > 0, ¯ ¯ ¯ ¯ n−1 n1 − 1 ¯ ¯ ¯ ¯ = 2 n1 < ǫ, if n > 2 ǫ −1 ¤ Remarks on limit proofs 1 The heart of a limit limits{n to ∞}1/nn/(n1)^2n/(n2)^2n/(2n1)^2 is equal to Sarthaks eConnect Largest Online Education Community \(\lim\limits_{n \to \infty}\left\frac 1n\frac n{(n1)^2}\frac n{(n2)^2}\frac n{(2n1)^2}\right to (1) 1/2 (2) 1 (3) 1/3 (4) 1/4 Login Remember Register Test

X lim n 1 2 n 0 n 1 2 1 4 1 8 1 16 1 32 a n 1 2 n n Limit of a Sequence Let be X lim n 1 2 n 0 n 1 2 1 4 1 8 1 16 1 32 a n 1 2 n n School Hayden High School;Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!When 1 2/n has n as a small number, assuming n is a Whole number, then If n = 1 1–2/n = 1 If n is large, eg n = 10^6 then 1 2/n = 1 2/1M =

1 Limiting distribution for a Markov chain In these Lecture Notes, we shall study the limiting behavior of Markov chains as time n!1 In particular, under suitable easytocheck conditions, we will see that a Markov chain possesses a limiting probability distribution, ˇ= (ˇSolve limits stepbystep \square! Where I've used the inequality of arithmetic and geometric means (a1*a2**an)^ (1/n) inf) (an) an=2/sqrt (n)1 lim (an)=1 (n>inf) bn < n^ (1/n) < an lim (bn)

2

2

(1 − x 1 − x 2 n ) = (1 Evaluate the following limits x → 1 limAnd the claim follows from the squeeze theorem (b) Prove that X1 n=1 1 2n n converges Solution Since lim n!1 n 2n = 0 as shown above, taking " = 1 10 in the de nition of the limit, we get that there is some N such that n 2n 1 10 for all n N Therefore, for n N, 1 2 n1n = 1 n n 2n 1 n 1 10 = 10 9 1 2 6Lim N → ∞ 1 2 2 2 3 2 N 2 N 3

2

Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection

 Last value is 1 2 = 1 10 Two bit integer can store only four (2 2) values 00, 01, 10 and 11 Last value is 11 2 = 3 10 Thus, when integer can stores N, values last value will be N1 because counting starts from zero n bit integer can store 2 n values Where last will be 2 n1 Example One byte can store 2 8 (256) values Where first is 0If the sum of the first ten terms of the series ( 1 3 5) 2 ( 2 2 5) 2 ( 3 1 5) 2 4 2 ( 4 4 5) 2 , is 16 5 m, then m is equal to 7 Let p = lim x → 0 ( 1 tan 2 8 For x ϵ R, f ( x) = log 9 For x ∈ R, x ≠ 0, x ≠ 1, let f 0 ( x) = 1 1 − x and f n 1 ( x) = f 0 ( f n ( x)), n = 0, 1, 2,The nth finite sum is 2 1/2^n This converges to 2 as n goes to infinity, so 2 is the value of the infinite sum

Search Q Limit Rules Tbm Isch

A Limit Involving Binomial Coefficients Lim N To Infty 1 N Sum K 1 N 1 K N Choose K 1 K Frac12 Mathoverflow

 If Sn = ∑ak for k∈k=1, n and lim(n→ ∞) an = a, then (n )(Sn 1) Sn)/√(∑k for k∈k=1, n asked in Limit, continuity and differentiability by Vikky01 ( 418k points) limitHint Show that lim n → ∞ n ln (1 n 3 n 2 n 2 c o s n ) = 2 Elaborating n ln ( 1 n 3 n 2 n 2 c o s n ) = n ln ( 1 n 1 / n 2 c o s ( n ) / n 2 ) = n a n a n l n ( 1 a n ) , So in this case, the limit has to be zero, because the denominator approaches infinity WAY faster *I also just noticed that factoring out the 2 n will also take out every single term in the numerator 2n4 = 2 (n2), so goodbye n2 term;

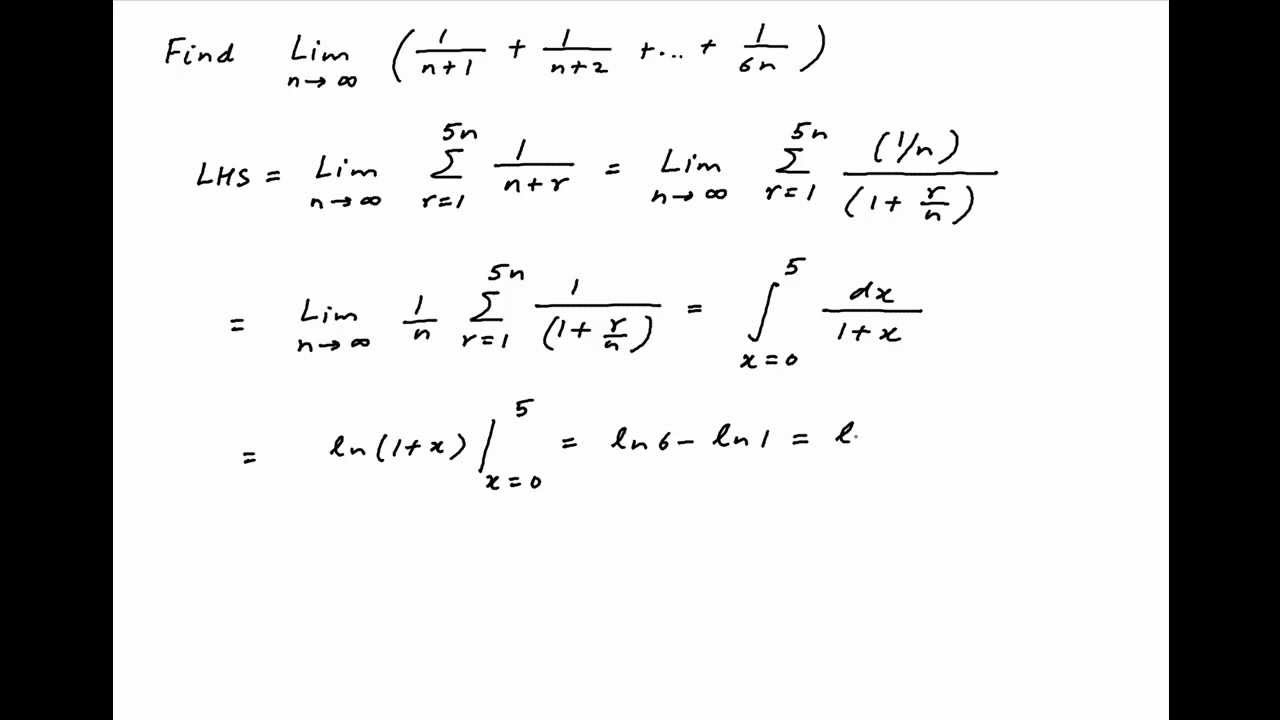
Find The Limit Of 1 N 1 1 N 2 1 N 3 1 6n As N Tends To Infinity Youtube

1

1 02 n Take the limit of each term Tap for more steps Split the limit using the Sum of Limits Rule on the limit as n n approaches 8 8 lim n → 8 1 − lim n → 8 02 n lim n → 8 ⁡ 1 lim n → 8 ⁡ 02 n Move the limit into the exponent lim n → 8 1 − 02 lim n → 8 n lim n → 8 ⁡ 1 02 lim n → 8 ⁡ n lim nThe power rule for differentiation states that if $n$ is a real number and $f(x) = x^n$, then $f'(x) = nx^{n1}$ $4x1\frac{d}{dx}\left(2x^3\right)$ The derivative of a function multiplied by a constant ($2$) is equal to the constant times the derivative of the functionNot a problem Unlock StepbyStep Extended Keyboard Examples Assuming limit refers to a discrete limit

Find The Limit Of 1 N 1 1 N 2 1 N 3 1 6n As N Tends To Infinity Youtube

Proof Of 1 1 N N E Youtube

Proof As with any infinite series, the sum is defined to mean the limit of the partial sum of the first n terms = as n approaches infinity By various arguments, one can show that this finite sum is equal to = As n approaches infinity, the term approaches 0 and so s n tends to 1 History Zeno's paradox This series was used as a representation of many of Zeno's paradoxes Limit of (n^2n)^(1/2)(n^3n^2)^(1/3) Thread starter karseme;$$ \lim_{x\to\ 1} \frac {x^21} {x1} = 2 $$ Calculating limit functions manually can take a lot of time and it requires experties Limit calculator with steps is designed to make you able to learn and practice quickly as you can find the limit table of values calculator easily

Also Known As Hysterical Calculus Online Presentation

Finding The Limit Of A Sequence N 2 N As N Approaches Infinity Youtube

 Here's an important limit from real analysis that gives quite a few people, including myself, a lot of trouble $$ \\lim_{n \\to \\infty}n^{1/n} = 1Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledLim ( (1/2)^n * 3^n (1 (1/2)^n) * 0, n=inf) WolframAlpha Rocket science?

What S The Limit Of 1 N 1 N As N Tends To Infinity Quora

2

Course Title MATH 2294; We will need to use Theorem 2 on this problem To this we'll first need to compute, lim n → ∞ ( − 1) n n = lim n → ∞ 1 n = 0 Therefore, since the limit of the sequence terms with absolute value bars on them goes to zero we know by Theorem 2 that, lim n → ∞ ( − 1) n n = 0Section 3 Sequences and Limits Definition A sequence of real numbers is an infinite ordered list a 1,a 2,a 3, a 4, where, for each n ∈ N, a n is a real number We call a n the nth term of the sequence Usually (but not always) the sequences that arise in practice have a recog

Pin On Math Videos

Math 101 Homework 2 Solutions 1 Evaluate The Limits N

Plugging in the next n into our partial sum formula we see that (n1)^2 = n^2n1, which is what we got earlier This shows that given a partial sum = n^2, all partial sums after that follows that pattern Then we simply do 13 = 2^2 to prove that there is a partial sum = n^2Et 2=2 2 Note that the requirement of a MGF is not needed for the theorem to hold In fact, all that is needed is that Var(Xi) = ¾2 < 1 A standard proof of this more general theorem uses the characteristic function (which is deflned for any distribution) `(t) = Z 1 ¡1 eitxf(x)dx = M(it)Thus the value of the infinite sum is a / (1r), and this also proves that the infinite sum exists, as long as r < 1 In your example, the finite sums were 1 = 2 1/1 3/2 = 2 1/2 7/4 = 2 1/4 15/8 = 2 1/8 and so on;

Math Exercises Math Problems Limit Of A Sequence

Unit 10 Sequences And Series Ppt Download

Limit (11/n)^n as n>infinity WolframAlpha Area of a circle? 1 A really elementary way is to observe the following an = n 2n = n n − 12n − 1 2n n − 1 2n − 1 = n n − 12n − 1 2n an − 1 = n 2(n − 1)an − 1 Let cn = n 2 ( n − 1) Prove for yourself that cn is smaller than 3 / 4 whenever n ≥ 3 Then what we have shown is an ≤ 3 4an − 1Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Find The Limit Of Frac N N 3 1 Frac 2n N 3 2 Dots Frac N Cdot N N 3 N Mathematics Stack Exchange

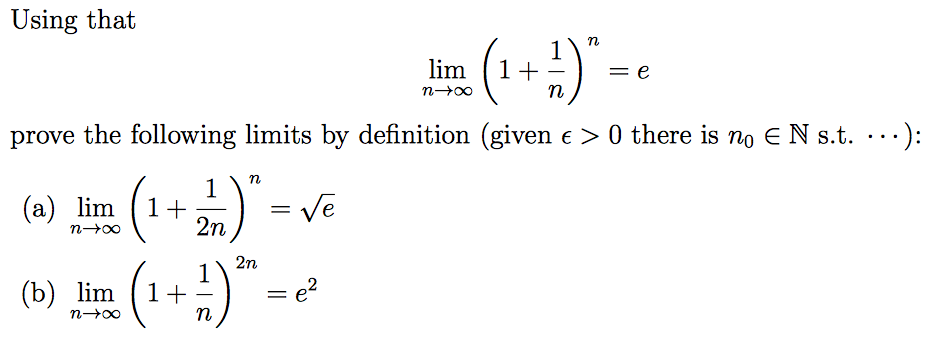
Using That Lim N Rightarrow Infinity 1 1 N N E Chegg Com

This way, sum starts with a zero and adds one element of the series to the overall sum at each iteration, starting with 1/n, then 1/n 2/(n1) and so on Share Follow answered Jan 17 '17 at 1845 RoaaGharra RoaaGharra 680 5 5 silver badges 18 18 bronze badges Add a comment Explanation n n2 n < n n2 1 < n n2 or 1 n 1 < n n2 1 < 1 n Here ∞ ∑ n=1 1 n 1 ≤ ∞ ∑ n=1 n n2 1 ≤ ∞ ∑ n=1 1 n but 1 ∞ ∑ n=1 1 n 1 = ∞ ∑ n=1 1 n = ∞ so ∞ ∑ n=1 n n2 1 is divergent Answer link2n n(n 1) 2;

Proof Of Lim N To Infty Sqrt N N 1 Mathematics Stack Exchange

Limit Theorems

MZn(t) = µ 1 t2 2n O µ 1 n3=2 ¶¶n!Weekly Subscription $199 USD por semana hasta cancelar Suscripción mensual $699 USD por cada mes hasta cancelar Suscripción anual $2999 USD por cada año hasta cancelar Therefore we subtract off the first two terms, giving ∞ ∑ n = 2(3 4)n = 4 − 1 − 3 4 = 9 4 This is illustrated in Figure Since r = 1 / 2 < 1, this series converges, and by Theorem 60, ∞ ∑ n = 0(− 1 2)n = 1 1 − ( − 1 / 2) = 2 3 The partial sums of this series are plotted in Figure (a)

2

How To Show That The Limit As N Approaches Infinity Of Log Log N Log N Is Zero Quora

 \\sum\limits_{n = 1}^\infty {\frac{{{n^2} 2}}{{{n^4}}}} \ is also a convergent series Recall that the sum of two convergent series will also be convergent Now, since the terms of this series are larger than the terms of the original series we know that the original series must also be convergent by the Comparison TestExponential Limit of (11/n)^n=e In this tutorial we shall discuss the very important formula of limits, lim x → ∞ ⁡ ( 1 1 x) x = e Let us consider the relation ( 1 1 x) x We shall prove this formula with the help of binomial series expansion We haveL'Hospital's Rule states that the limit of a quotient of functions is equal to the limit of the quotient of their derivatives lim n → ∞ n 2 n = lim n → ∞ d d n n d d n 2 n lim n → ∞ ⁡ n 2 n = lim n → ∞ ⁡ d d n n d d n 2 n Find the derivative of the numerator and denominator Tap for more steps

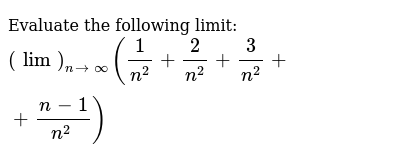
Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N

Direct And Limit Comparison Test Ppt Download

 Compare it to that using the limit comparison test √n1 n21 1 n3 2 = ( √n 1 n2 1) n3 2 1 = n3 2√n 1 n2 1 = n3 2√n√1 1 n n2(1 1 n2) = √1 1 n 1 1 n2 The limit as n → ∞ is 1, which is positive Since ∑ 1 n3 2 converges (pseries), so does ∑( √n 1 n2 1 Answer linkAnswer to Determine the limits of the following sequences If the limit does not exist, write DNE a) an = n^3/n^3n^2n1 b) bn = (4^n)(5^(n))The limit of the sequence given is represented as lim n→∞(1− 2 n)n lim n → ∞ ( 1 − 2 n) n Evaluating this limit utilizes lim n→∞(1− a n)n = e−a lim n → ∞ ( 1 − a n) n

1

Search Q Limit N Tends To Infinity 1 N Tbm Isch

 We know that 123n = n(n1)/2 ==> lim 2n^2/n(n1) = 2lim n^2/ lim n^2n Let us divide by the highest power n^2 ==> 2lim (n^2/n^2) / lim n^2(11/n) Reduce similar ==> 2 lim(1)/lim (11/n2n6 = 2 (n3), so goodbye n3 term, and it should go that way all the way downE as the limit of (1 1=n)n Math 122 Calculus III D Joyce, Fall 12 This is a small note to show that the number e is equal to a limit, speci cally lim n!1 1 1 n 1 n = e Sometimes this is taken to be the de nition of e, but I'll take e to be the base of the natural logarithms

How To Prove That The Limit Of 2n 1 3n 7 As N Approaches Infinit Math Books Math Videos Math

Video 2533 Limit Of Sequence 1 1 N 2 N Practice Youtube

Easy as pi (e) Unlock StepbyStepSo, for n 2, 0 n 2n 2 n 1;

Show That Lim N Tends To Infinity 1 N 1 N 1 1 N 2 1 3n Log 3 Brainly In

Mathematics Mathematical Analysis Special Sequences And Divergence Steemit

2

What Is The Limit Of N Infinity N 2 N Quora

What Is The Limit Of 2 N 1 3 N 1 2 N 3 N As N Tends To Infinity Quora

What Is Lim 3 N 2 N 1 2n When N Tends To Infinity Quora

Convergence Of A Sequence As N Tends To Infinity Mathematics Stack Exchange

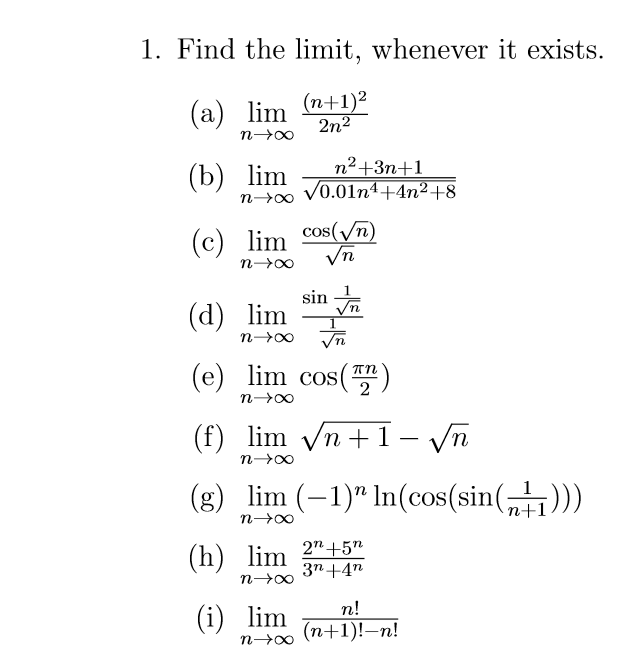
Find The Limit Whenever It Exists A Lim N Chegg Com

Answered Series 23 56 Determine Whether The Bartleby

Compute The Limit Of The Recursive Sequence An 1 An An 1 2 Stumbling Robot

Limit Comparison Test For Series 1 N 2 Log N Converge Or Diverge Mathematics Stack Exchange

1 Use The Definition Of Limit To Show That Lim 2n 1 Chegg Com

2

In Showing Integer Sum 1 2 3 N By L Hopital Rule Why They Take Lim As R Approaches To 1 In One Of Steps Why 1 Mathematics Stack Exchange

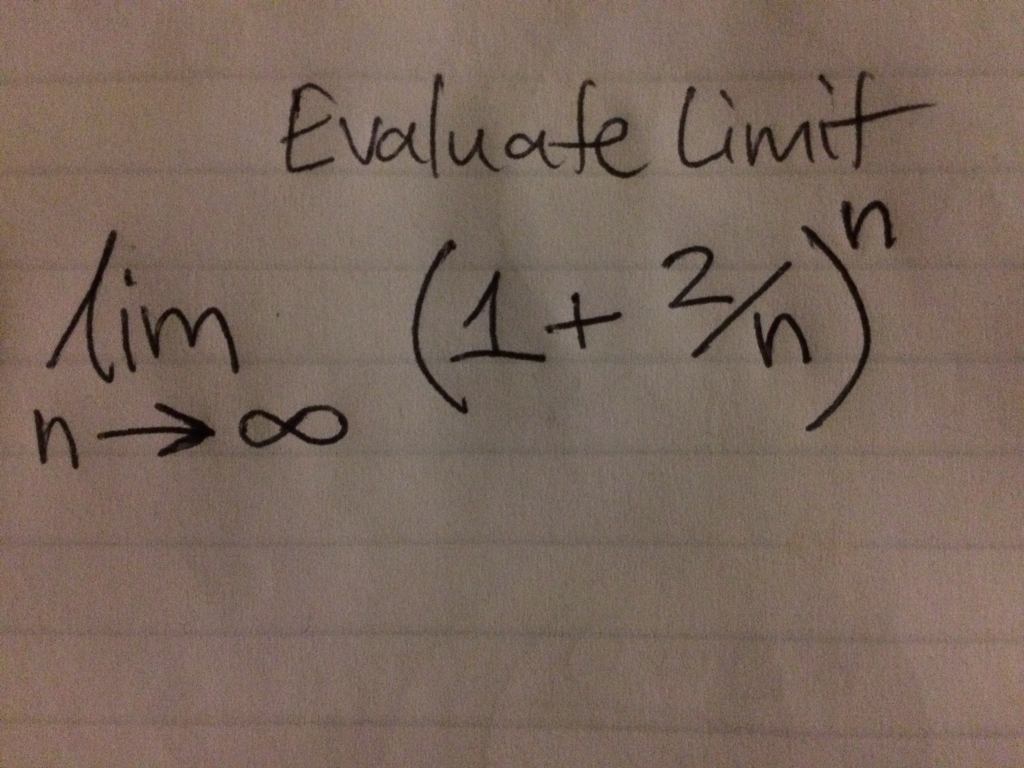
Evaluate Limit Lim N Rightarrow Infinity 1 2 N N Chegg Com

Real Analysis Prove That This Sequence Is A Cauchy Sequence Calculate Limit Cheatatmathhomework

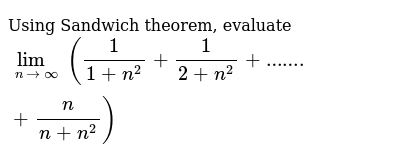
Using Sandwich Theorem Evaluate Lim N Oo 1 1 N 2 1 2 N 2

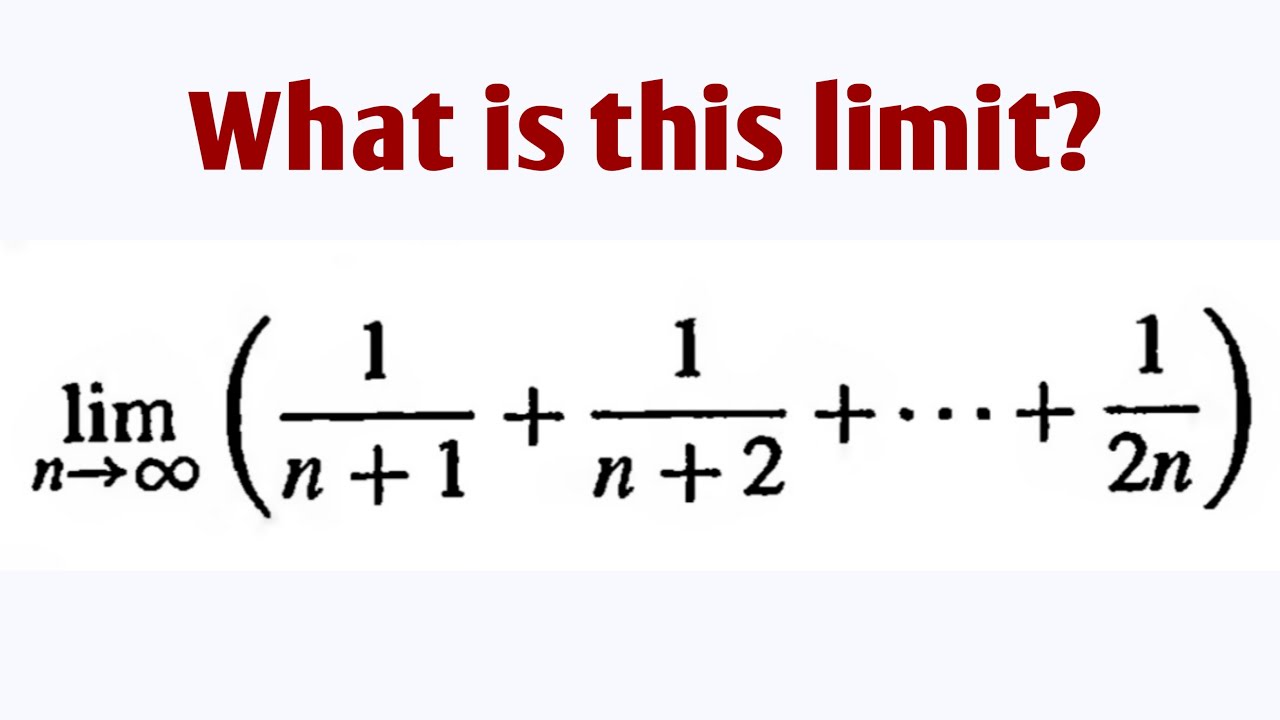
Lim 1 N 1 1 N 2 1 2n What Is This Limit Youtube

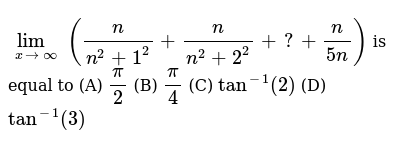
Lim Xrarroo N N 2 1 2 N N 2 2 2 N 5n 2 Is Equal To

Answered In Exercises Series Converges Or Bartleby

Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N

Infinite Sequences And Series Ppt Video Online Download

5 Use The Definition Of The Limit Of A Sequence Gauthmath

L Hopital S Rule Limit At Infinity Example Video Khan Academy

Lim N Gtoo 1 2 3 4 5 6 2n Sqrt N 2 1 Sqrt 4n 2 1 1 1 3 2

Limit Limit N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community

Learn Calculus Daily Calculus Problems Calculus Tutorials Sigma Notation Summation Rules Limits At Infinity

Mth3101 Advanced Calculus Chapter 2

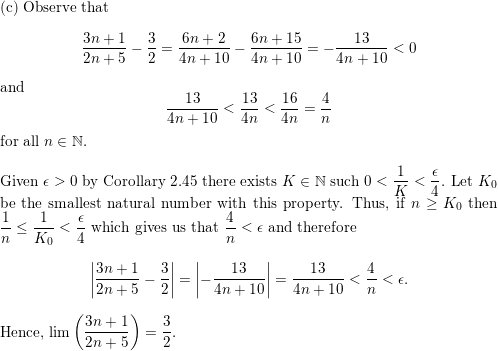
Use The Definition Of The Limit Of A Sequence To Establish The Following Limits A Math Lim Left Frac N N 2 1 Right 0 Math B Math Lim Left Frac 2 N N 1 Right 2 Math C Math Lim Left Frac 3 N 1 2 N 5 Right Math 3 2

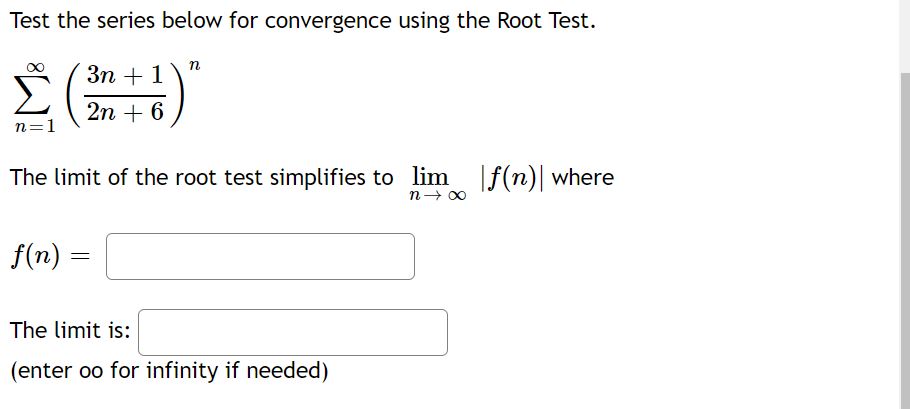
Answered Test The Series Below For Convergence Bartleby

Answered Ries Diverges 23 56 Determine Whether Bartleby

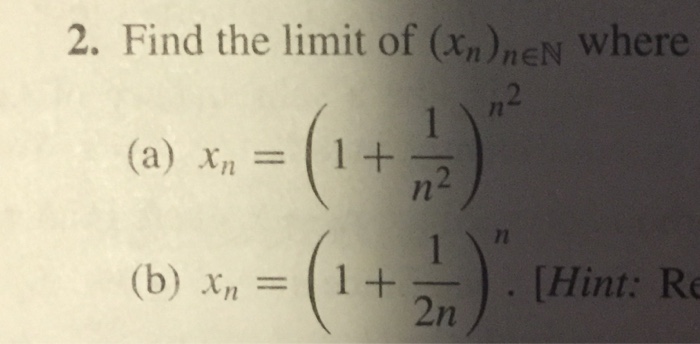
Find The Limit Of X N N N Where X N 1 Chegg Com

In Questions 1 8 Find The Limit Of The Sequence Sin N Cos N 2 37 N Sin N 3 4 Cos Rn 5 N Sin N O Cos N N 9 If

Content Limit Of A Sequence

Table 1 From The Continuum Limit Of A N 1 2 Spin Chains Semantic Scholar

N 1 2 2 2 3 2 N 2n 3 Is Equal To

An 1 2 N 1 N Determine Whether The Sequence Converges Or Diverges Youtube

The Limit When N Tends To Infinity Of The Series Frac Sqrt N Sqrt N 3 Frac Sqrt

Take For Granted That The Limit Lim 1 1 N N Chegg Com

Example 25 Find Integral X2 1 Dx As Limit Of A Sum Examples

1234n Formula

Find The Limit Of Each Sequence If It Exists Justify Chegg Com

Math 2260 Written Hw 12 Solutions

Evaluating Frac1 N 2 1 2 Frac2 N 2 2 2 Dots Frac N N 2 N 2 Using Riemann Sum Mathematics Stack Exchange

2

2

What Is Math Lim Limits N To Infty Left 1 Frac 1 N Right N Math Quora

Find The Limit If It Exists For Each Of The Chegg Com

Limit Comparison Test Video Khan Academy

Asymptotic Notation How To Prove That N 2 W Nlogn Stack Overflow

Chapter Ii The Limit Of A Sequence Of Numbers Definition Of The Number E Pdf Free Download

2

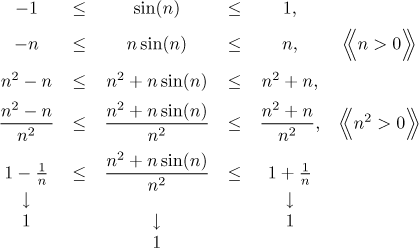
Math Tutor Sequences Solved Problems Limits

Limit Replace 1 By 0 Mathematics Stack Exchange

How To Evaluate Lim N Tends To Infinty 2 N 1 2 N 1 Without The Hospital Rule Quora

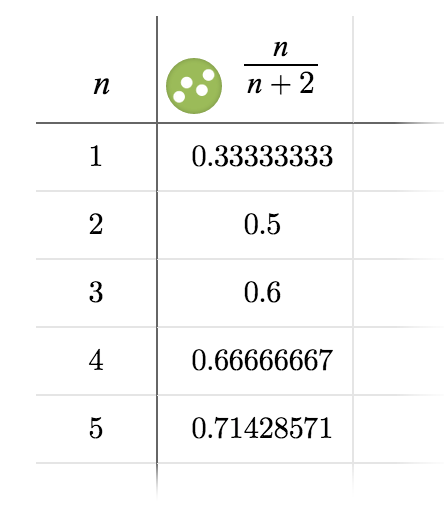
Write Out The First Five Terms Of The Sequence Determine Whether The Sequence Converges And If So Find Its Limit Left Frac N N 2 Right

Chapter 3 Cbu

In Questions 1 8 Find The Limit Of The Sequence Sin N Cos N 2 37 N Sin N 3 4 Cos Rn 5 N Sin N O Cos N N 9 If

Science Infinite Series Module Units Unit 1 1 1 Infinite Sequences 1 1 06 Limit Laws Example Ubc Wiki

Chapter 1

Ism Et Chapter 8

2

Also Known As Hysterical Calculus Online Presentation

2

Science Infinite Series Module Units Unit 1 1 1 Infinite Sequences 1 1 06 Limit Laws Example Ubc Wiki

Ma2108s Tutorial 5 Solution

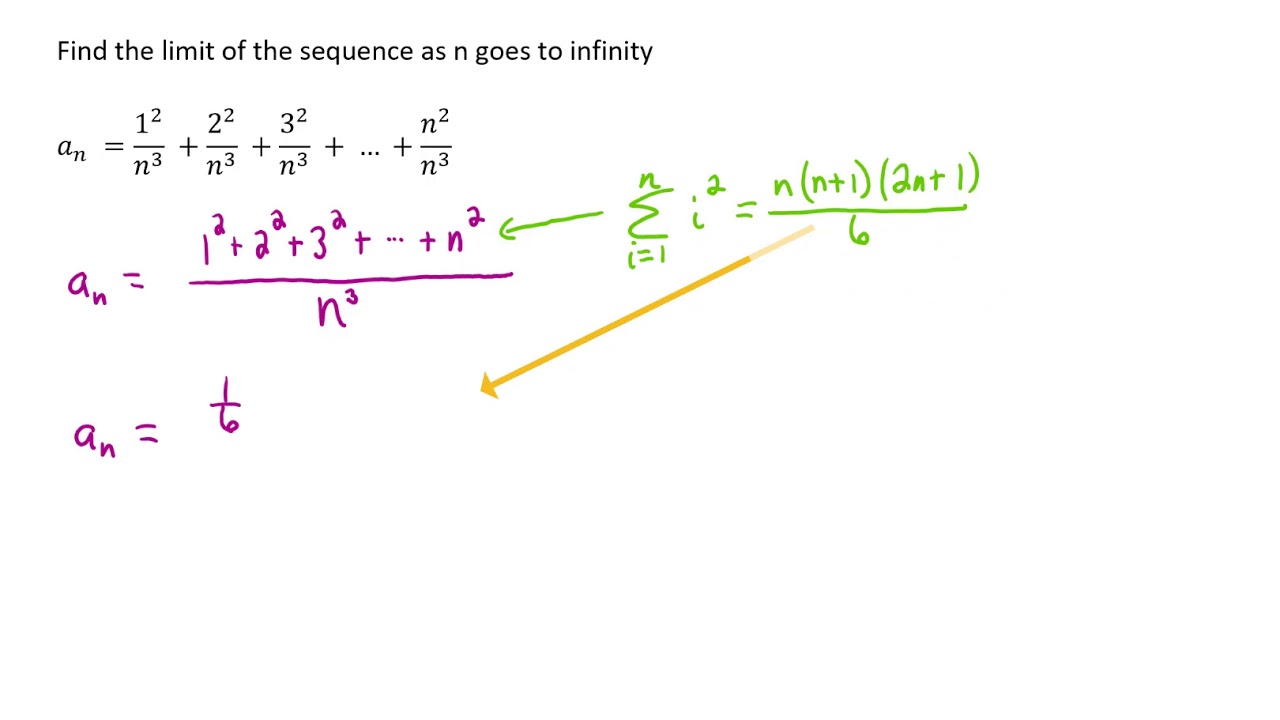
Find The Limit Of 1 N 3 2 2 N 3 3 2 N 3 N 2 N 3 As N Goes To Infinity Sequences 2 Youtube

Solutions For Final Exam Mathematics And Computer Science

A Consider The Sequence With Terms 2n In 1 An Chegg Com

Lim N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community

Limit Of The Sequence A N N Left Sin Left Frac 1 N 3 N 2 Right Sin N Right Mathematics Stack Exchange

Limit Of Sequence Lim N 1 Cos 2 N Physics Forums

Lim N Infinity N N 2 1 Youtube

Prove The Following Using The Definition Of A Limit Chegg Com

Incoming Term: (1+2/n)^n limit, limit (1+2/n)^n as n- infinity, limit of sequence (1+2/n)^n, sqrt(n^2+1)-n limit, limit of 1/2^n as n goes to infinity, n^2(1-cos(1/n)) limit, limit ln(2 n/n+1), limite 2^n/3^n+1, what is the limit of (1+1/n)^n, 1/2^n limit,